백준 2007 수들의 합 3
https://www.acmicpc.net/problem/2007
2007번: 수들의 합 3
첫 번째 줄에는 N(2 ≤ N ≤ 100) 이 입력된다. 두 번째 줄에는 N×(N-1)/2개의 합들이 주어진다. 입력으로 주어지는 합은 절댓값이 1,000,000보다 작거나 같은 정수이다.
www.acmicpc.net
풀이
먼저 정수 쌍을 저장하고 오름차순으로 정렬합니다.
정수 쌍을 다음과 같이 정의하겠습니다.
A1 , A2 ... , An(n-1)/2 (Ai ≤ Aj)
그리고 구해야하는 원래 N개의 값은 다음과 같이 정의 하겠습니다.
B1 , B2 ... , Bn (Bi ≤ Bj)
먼저 A1 = B1 + B2 라는 사실을 알 수 있습니다.
(가장 작은 두개의 수를 합치면 가장 작은 값이 나오기때문입니다.)
그리고 A2 = B1 + B3 입니다.
(B2 + B3 은 B1 < B2 이므로 A2가 될수 없습니다. 다른 경우도 마찬가지)
그리고 A3 = B1 + B4 라고 생각할 수도 있지만...
B2 + B3도 A3의 후보가 될 수 있기 때문에 A3부터는 규칙이 성립하지 않습니다.
(ex 1 3 4 10)
A1 = B1 + B2 , A2 = B1 + B3 이므로
A1 + A2 = 2B1 + B2 + B3 이 만들어지고 해당식에서 B2 + B3만 정하면 B1의 값을 얻을 수 있습니다!!
(정답은 정수 값이므로 A1 + A2 - B2 - B3 가 짝수여야만 성립됩니다.)
B2 + B3는 A값중 하나이므로 Ai (3 ≤ i ≤ 7)인 모든 A를 넣어 볼 수 있습니다.
(i ≥ 2인 이유는 A1 , A2는 앞에서 사용했기 때문이고 ,i ≤ 7인 이유는 B3+ B4보다는 커질수 없기 때문입니다.)
이제부터 이야기가 길어지므로 그림을 그려보겠습니다.
N=5인 경우 입니다.

B1 + B2= A1이고 B1 + B3= A2입니다.
우리는 이미 알고 있으므로 체크를 하겠습니다.

B2 + B3는 A값들중 하나로 정한다고 했기 때문에 값을 구했다고 처리하겠습니다.
그리고 위의 설명했드시 B2 + B3를 구하면 B1을 구할 수 있습니다.

현재 갖고 있는 정보를 통해
A1 - B1 = (B1 + B2) - B1 = B2 를 이용해 B2를 구할 수 있고
마찬가지로 A2 - B1 = (B1 + B3) - B1 = B3 를 이용하면 B3를 구할 수 있습니다.

현재 표시하지 않은 A값들을 확인해보면 B1 + B4보다 작은 값이 없다는 것을 알수 있습니다!!
즉 현재 남은 A값 중 가장 작은수는 B1 + B4라는 사실을 알 수 있습니다.
우리는 이미 B1을 알고 있기 때문에 자연스럽게 B4의 값을 알 수 있습니다.

B1, B2, B3, B4를 모두 알고 있기 때문에 자연스럽게
B1 + B4 ,B2 + B4 ,B3 + B4의 값을 모두 알 수 있게 되었습니다.
위에 값들이 A에 있는지 확인 후 체크를 해줍니다.
(막약 A에 해당 값들이 없다면 유효한 답이 아닙니다.)

위와 똑같습니다. 현재 표시하지 않은 A값들을 확인해보면 B1 + B5보다 작은 값이 없다는 것을 알수 있습니다.
즉 현재 남은 A값 중 가장 작은수는 B1 + B5라는 사실을 알 수 있습니다.
우리는 이미 B1을 알고 있기 때문에 자연스럽게 B5의 값을 알 수 있습니다.
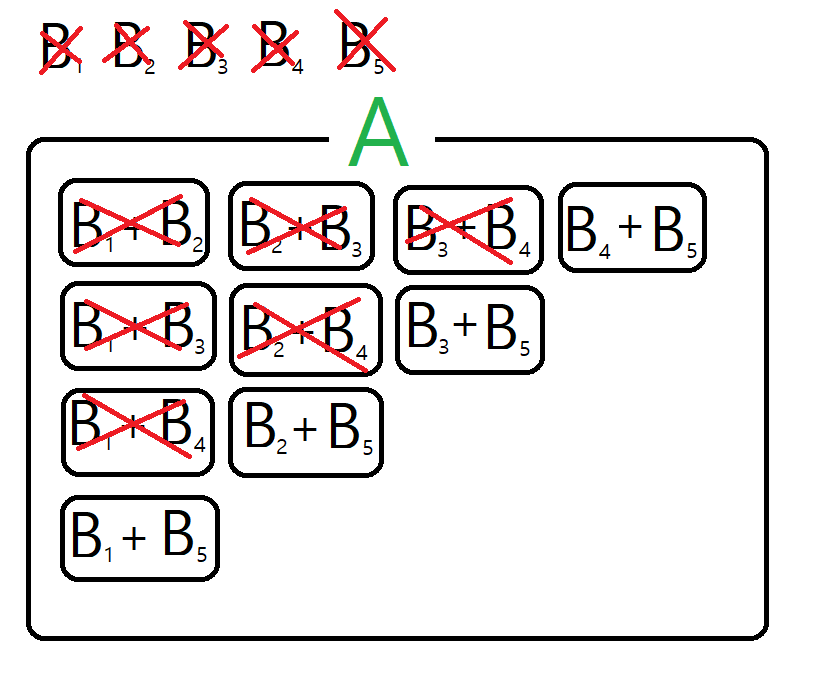
B1, B2, B3, B4, B5를 모두 알고 있기 때문에 자연스럽게
B1 + B5 ,B2 + B5 ,B3 + B5, B4 + B5의 값을 모두 알 수 있게 되었습니다.
위에 값들이 A에 있는지 확인 후 체크를 해줍니다.
(막약 A에 해당 값들이 없다면 유효한 답이 아닙니다.)

조금 복잡한 로직입니다.
이해하기 어렵다면 코드를 참고하는 것을 추천드립니다.
단 주의 할점이 있습니다.
N = 2인 경우는 위의 방법이 적용되지 않습니다.
괜찮습니다. 다행이 어려운 일이 아닙니다.
A1 = B1+B2라는 경우 밖에 없기 때문에
B1값을 임의로 정한후 B2를 구하면 됩니다.
코드
#include <bits/stdc++.h>
using namespace std;
#define endl "\n"
#define int long long
#define float double
int N;
vector<int> A;
map<int, int> hasA;
bool HasA(int v)
{
if (hasA.find(v) != hasA.end())
if (hasA[v] > 0)
return true;
return false;
}
int B[101];
vector<int> Result;
void F(int n, int m)
{
if (n >= A.size())
{
for (int i = 0; i < m; i++)
Result.push_back(B[i]);
return;
}
if (!HasA(A[n]))
F(n + 1, m);
else
{
B[m] = A[n] - B[0];
for (int i = 0; i < m; i++)
if (!HasA(B[i] + B[m]))
return;
for (int i = 0; i < m; i++)
hasA[B[i] + B[m]]--;
F(n + 1, m + 1);
for (int i = 0; i < m; i++)
hasA[B[i] + B[m]]++;
}
}
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
cin >> N;
A.resize(N * (N - 1) / 2);
for (int i = 0; i < N * (N - 1) / 2; i++)
{
cin >> A[i];
hasA[A[i]]++;
}
if (N == 2)
{
B[0] = -1000000;
B[1] = A[0] - B[0];
cout << min(B[0], B[1]) << " " << max(B[0], B[1]) << endl;
return 0;
}
sort(A.begin(), A.end());
for (int i = 2; i < 7; i++)
{
if (Result.size())
break;
int temp = (A[0] + A[1] - A[i]);
if (temp % 2)
continue;
B[0] = temp / 2;
B[1] = A[0] - B[0];
B[2] = A[1] - B[0];
hasA[A[i]]--;
hasA[A[0]]--;
hasA[A[1]]--;
F(0, 3);
hasA[A[i]]++;
hasA[A[0]]++;
hasA[A[1]]++;
}
if (Result.size())
{
for (int i = 0; i < Result.size(); i++)
cout << Result[i] << " ";
cout << endl;
}
else
cout << "Impossible" << endl;
return 0;
}
-----------------------------------------------------------------------------------------------------------------------------------
질문은 언제나 환영합니다.