이진탐색트리는 다음과 같은 조건을 만족하는 트리다.
1. 노드의 왼쪽에는 자신보다 낮은 값을 가진 노드가 들어간다.
2. 노드의 오른쪽에는 자신보다 높은 값을가진 노드가 들어간다.
3. 왼쪽 및 오른쪽 하위트리도 이진탐색트리여야한다.
4. 중복값을 허용하지 않는다.
이진탐색트리에 데이터가 들어가면 어떻게 구성되는지 살펴보자.
20 10 30순으로 입력하면 트리의 모양이 이렇게될거다.

데이터가 이쁘게들어와서 균형잡힌트리가 나왔다.
그렇지만 데이터가 이렇게 형편좋게 들어올리는없다.
10 20 30순으로만 들어와도 이렇게될것이다.

해당 트리에서 특정값 v를 찾는다고해보자.
균형잡힌 트리라면 O(logN)이면 탐색되겠지만
위의 그림처럼 불균형한 트리라면 O(N)까지 걸릴 수 있다.
트리를 항상 균형잡힌 상태로 유지할 방법이 없을까?
해당 문제를 해결한 트리가 바로 레드블랙트리다.
레드블랙트리는 다음과같은 규칙을 따른다.
1.노드는 검정색노드와 빨간색노드로 이루어져있다.
2.루트노드는 검정색노드다.
3.모든 자식노드는 검정색노드다. (만약 자식노드가 NULL이라면 검정색노드로 간주한다.)
4.빨간색노드의 자식노드는 검정색노드다.
5.새롭게 추가되는 노드는 빨간색노드다.
하지만 해당 규칙을따라서 이진탐색트리에 데이터를 입력하다보면 이상한 문제에 봉착하게될것이다.
10 20 30을 입력해보자.
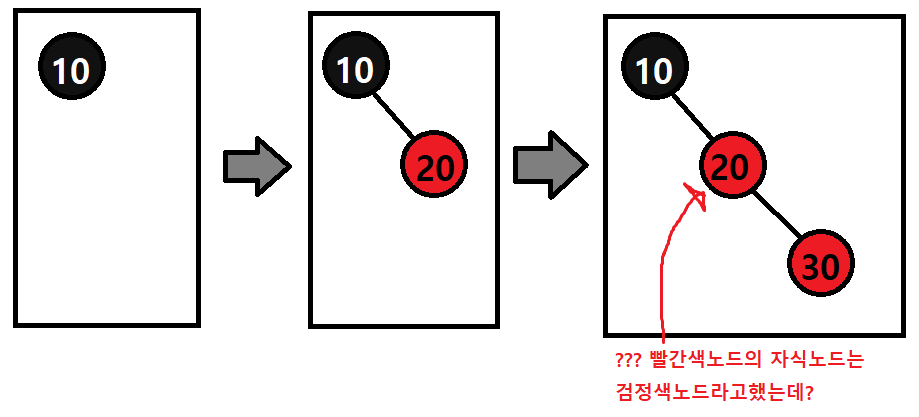
자식노드와 부모노드가 둘다 빨간색노드다.
4번 규칙인 "빨간색노드의 자식노드는 검정색노드다."라는 규칙을 명백히 위반하고 있다.
해당 상태를 더블레드라고 부른다.
레드블랙트리에서는 더블레드상태가 되었을때 해결하는 방법 2가지를 제시해주고있다.

노드를 다음과 같이 정의하겠다.
현재노드는 N
부모노드는 P
조상노드는 G
삼촌노드는 U


다음은 더블레드가 발생한 상황이다.
두개의 이미지의 차이점을 살펴보면 U의 색상이 다른데
U의 색상에 따라서 처리해야하는 방식이 다르기 때문이다.
U의 색상이
빨간색이면 -> Recoloring연산수행
검정색이면 -> Restructuring연산수행
Recoloring와 Restructuring에 대해서 살펴보자.
1) Recoloring

1.P와 U를 검정노드로 만든다.
2.G를 빨간노드로 만든다.(G가 루트노드라면 검정노드로 설정한다.)
2번에서 G를 빨간색으로 바꾸기때문에 더블레드 상태가 될수가있다.
G에서부터다시 Recoloring이랑 Restructuring중에서 알맞는 연산을 실행하면된다.
2) Restructuring

1.N P G를 오름차순으로 정렬해서 가운데 값을 구한다.
2.가운데값을 부모로 만들고 나머지는 자식노드로 만들어서 트리를 재구성한다.
3.새롭게 부모가된노드는 검정노드로 만들고 자식노드는 빨간노드로 만든다.
레드블랙트리의 대략적인 설명은 끝났다.
아래는 레드블랙트리를 구현한 코드다.
#include <bits/stdc++.h>
#pragma warning(disable:4996)
using namespace std;
#define endl "\n"
#define int long long
#define float long double
#define Debug(a,b) cout << a << " " << b << endl
#define Init(a,b) memset(a,b,sizeof(a))
const float INF = 1e18;
const int Dic[8][2] = { {0,-1},{1,0},{0,1},{-1,0} ,{1,1},{-1,-1},{1,-1},{-1,1} };
////////////////////////////////////////////////////////////////////////
struct Node
{
public:
int color;
int v;
Node* left;
Node* right;
Node* parent;
Node()
{
}
Node(int pColor,int pV, Node* pLeft,Node* pRight, Node* pParent)
: color(pColor), v(pV), left(pLeft), right(pRight), parent(pParent)
{
}
};
class RedBlackTree
{
public:
Node* rootNode;
RedBlackTree() : rootNode(NULL)
{}
void Insert(int v)
{
Node* tempNode = rootNode;
Node* tempParents = rootNode == NULL ? NULL : rootNode->parent;
while (tempNode != NULL)
{
tempParents = tempNode;
if (tempNode->v > v)
{
if (tempNode->left == NULL)
{
tempNode->left = new Node(1, v, NULL, NULL, tempParents);
break;
}
tempNode = tempNode->left;
}
else
{
if (tempNode->right == NULL)
{
tempNode->right = new Node(1, v, NULL, NULL, tempParents);
break;
}
tempNode = tempNode->right;
}
}
if (rootNode == NULL)
{
rootNode = new Node(1, v, NULL, NULL, tempParents);
rootNode->color = 0;
}
CheckDoubleRed(tempNode);
}
bool HasValue(int v)
{
Node* tempNode = rootNode;
while (tempNode != NULL)
{
if (tempNode->v == v)
return true;
if (tempNode->v > v)
tempNode = tempNode->left;
else
tempNode = tempNode->right;
}
return false;
}
private:
void CheckDoubleRed(Node* pN)
{
if (pN == NULL || pN->parent == NULL || pN->parent->parent == NULL)
return;
Node* N = pN;
Node* P = pN->parent;
Node* G = P->parent;
Node* U = G->left == P ? G->right : G->left;
int uColor = U == NULL ? 0 : U->color;
int pColor = P->color;
if (pColor == 1 && uColor == 1)
Recoloring(N, P, U, G);
else if (pColor == 1 && uColor == 0)
Restructuring(N, P, U, G);
}
void Recoloring(Node* pN, Node* pP, Node* pU, Node* pG)
{
pP->color = 0;
if(pU != NULL)
pU->color = 0;
pG->color = 1;
if (pG == rootNode)
pG->color = 0;
CheckDoubleRed(pG);
}
void Restructuring(Node* pN, Node* pP, Node* pU, Node* pG)
{
Node* Gp = pG->parent;
Node* a = pN;
Node* b = pP;
Node* c = pG;
if (a->v > b->v)
swap(a, b);
if (b->v > c->v)
swap(b, c);
if (a->v > b->v)
swap(a, b);
a->parent = b;
if (a->left == b)
a->left = NULL;
if (a->right == b)
a->right = NULL;
if (pG == rootNode)
rootNode = b;
b->parent = Gp;
b->left = a;
b->right = c;
c->parent = b;
if (c->left == b)
c->left = NULL;
if (c->right == b)
c->right = NULL;
b->color = 0;
a->color = 1;
c->color = 1;
}
};
int32_t main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
RedBlackTree redBlack = RedBlackTree();
while (true)
{
int a, b;
std::cin >> a >> b;
if (a == 1)
redBlack.Insert(b);
else
{
if (redBlack.HasValue(b))
std::cout << "Has" << endl;
else
std::cout << "Not" << endl;
}
}
}